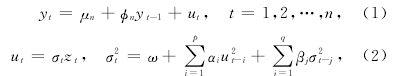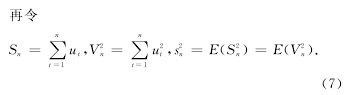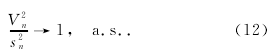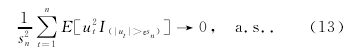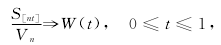0引言
DICKEY与FULLER提出了带有独立同分布且方差有限的误差项情形下的单位根检验,即着名的Dickey-Fuller检验.近30年来,该检验被广泛地应用于计量经济学的非平稳性检验.然而,现实的计量经济模型中经常会遇到误差项不具有独立同分布这一特殊的属性.因此该检验被大量地推广以适应各种不同的情形,如相依的误差、异方差或重尾等.ARCH模型和GARCH模型被广泛地应用于刻画金融市场的波动性,其反映了金融市场中的相依性和重尾属性.本文将讨论由GARCH误差驱动的单位根过程的检验问题。
考虑如下带有广义自回归条件异方差(GARCH误差项)和常数趋势项的单位根过程:
这里的μn,?n为2个未知参数,μn为随着n变动的参数,?n=1,y0 =0,p和q为已知的非负整数,ω>0,对i=1,2,…,p,αi≥0,对j=1,2,…,q,βj≥0,且更新项{zt}是数学期望为0,方差为1的独立同分布随机变量序列.当μn=0,且?n=1时,式(1)即是熟知的单位根模型.对于带有GARCH误差项的单位根模型,已经有许多学者对其进行了深入的研究,如文献[5]讨论了GARCH(1,1)误差下的单位根过程的最小二乘估计和极大似然估计;文献[6]讨论了同一模型的一步局部拟似然估计.这2篇文章中的估计量的渐近分布都是在Eu2t< ∞与Ez4t< ∞的条件下得到的.文献[7]在误差项与更新项都只有有 限 二 阶 矩 的 条 件 下 得 到 了 这 一 模 型 的Dickey-Fuller检验统计量的渐近分布.文献[8]讨论了带有ARFIMA-GARCH误差的单位根过程的检验问 题;文 献 [9]利 用LAD估 计 讨 论 了 带 有GARCH(p,q)误差项的单位根过程,并在误差项与更新项都只有有限二阶矩存在的条件下推导出了估计量的渐近分布.当μn=0,且?n <1为固定常数时,式(1)即为平稳过程.这时的最小二乘估计量^?n的极限分布与单位根情形是完全不同的.当μn ≠0且?n=1时,模型(1)为带有常数趋势的单位根过程,虽然只是形式上的微小区别,但是其估计量的渐近分布性质与μn=0的情形是非常不同的.关于这个模型的统计推荐细节参见文献[10].本文的目的是在误差项与更新项都只有有限二阶矩存在的条件下,研究带有GARCH(p,q)误差与常数趋势的模型(1)的Dickey-Fuller检验统计量的渐近分布.这个结果推广了文献[7]的结果.
1主要结果
1.1模型与假设
假设y1,y2,…,yn为观察值.则模型(1)中的参数?n的最小二乘估计量为
如文献[11]所示,假设A意味着{ut}是严格平稳序列且其二阶矩Eu2t=σ2u< ∞.且s2n=nσ2u,然而可能对任意小的δ>0,有Eu2+δt= ∞.
1.2 Dickey-Fuller检验统计量的渐近分布
本文的主要结果如下.定理1令yt为模型(1)与(2)所产生的数据,且假设A成立.那么
2定理的证明
2.1几个引理
首先需要下面2个引理.引理1假设A成立,那么
理2假设A成立,那么当n→ ∞时,对所有的ε>0,有
引理1与引理2的证明详见文献[11].
2.2定理1的证明
注意到{ut}是一个鞅差序列.由引理1、引理2和文献[12]的定理4.1,有
这里的[x]表示不大于x的最大的整数,“?”表示在被赋予Skorohod拓扑的 空间上的弱收敛,且W(t)为标准的布朗运动.再由引理1,有
参考文献(References):
[1]DICKEY D A,FULLER W A.Distribution of the es-timators for autoregressive time series with a unit root[J].J Amer Statist Assoc,1979,74:427-431.
[2]DICKEY D A,FULLER W A.Likelihood ratio statis-tics for autoregressive time series with a unit root[J].Econometrica,1981,49:1057-1072.
[3]PHILLIPS P C B,XIAO Z.A primer on unit root tes-ting[J].J Econom Surv,1998(12):423-469.
[4]STOCK J H.Unit root,structural breaks and trends[M]//Handbook of Econometrics.Amsterdam:Elsevi-er,1994:2739-2841.
[5]LING S,LI W K,MCALEER M.Estimation and tes-ting for unit root processes with GARCH(1,1)er-rors:theory and Monte Carlo evidence[J].Economet-ric Reviews,2003,22:179-202.
[6]LING S,LI W K.Asymptotic inference for unit rootprocesses with GARCH(1,1)errors[J].EconometricTheory,2003,19:541-564.
[7]WANG G.A note on unit root tests with heavy-tailedGARCH errors[J].Statistics and Probability Letters,2006,76:1075-1079.
[8]WANG G.Unit root testing in the presence of ARFI-MA-GARCerrors[J].Appl Stochastic Models BusInd,2011,27:421-433.
[9]LI G,LI W K.Least absolute deviation estimation forunit root processes with GARCH Errors[J].Econo-metric Theory,2009,25:1208-1227.
[10]HAMILTON J D.Time Series Analysis[M].NewJersey:Princeton University Press,1994.
[11]YUAN Yuze,ZHANG Rongmao.Estimation fornearly unit root processes with GARCH errors[J].Appl Math J Chinese Univ:Ser B,2010,25(3):297-306.
[12]HALL P,HEYDE C C.Martingale Limit Theory andIts Application[M].New York:Academic Press,1980.