摘要:建立了径向基函数配点法求解类拉普拉斯方程定解问题的方法。将求解域依据系数张量为分片常量来分解为若干子域。在每个子域上分别利用所布置的中心点建立用径向基函数表达的近似待解函数。在每个子域内及子域边界与外边界重合部分的配置节点上分别利用类拉普拉斯方程和定解条件建立近似解函数的待定系数满足的配点方程组,在相邻子域的分界线的配置节点上利用相容条件建立待定系数满足的配点方程组。方程组联立求解就得到了整个域上的近似解。算例计算表明该方法求解问题简捷有效,算法具有很高的精度。
关键词:数值模拟; 径向基函数配点法; 相容条件; 类拉普拉斯方程;
Abstract:The radial basis function collocation method is established to solve the definite solution of quasi-Laplacian equation.The solution domain is decomposed into several subdomains according to the coefficient tensor as the sharding constant.In each subdomain,an approximate unsolved function expressed by the radial basis function is established by using the center points.In each subdomain and on the configuration nodes where the boundary of the subdomain overlaps with the outer boundary,quasi-Laplace equation and the definite solution condition are respectively used to establish the collocation point equations that the undetermined coefficients of the approximate solution function satisfy,and the compatibility condition is used to establish the collocation point equations that the undetermined coefficients satisfy on the configuration nodes of the boundary of the adjacent subdomain.The simultaneous solution of the equations gives the approximate solution over the whole domain.Numerical examples show that the method is simple and effective,and the algorithm has high precision.
Keyword:numerical simulation; radial basis function collocation method; compatibility conditions; quasi-Laplace equation;

目前,求解偏微分方程近似解时广泛使用的方法主要有有限元法和有限差分法等。这些方法的一个显著特征是必须依赖网格,这使得它们在用于实际工程计算时会出现计算量大和算法实现较为困难等问题。为了寻找能够克服这些缺点的数值计算方法,学者们研究出了一类免网格的微分方程数值求解新方法---无网格法。
径向基函数(Radial Basis Function,简称RBF)配点法是众多无网格法中的一种,具有方法直接、原理简单、收敛速度快、无须数值积分、节点布置灵活等特点,因而该方法具有易于理解、编程容易、计算速度快、适用问题广、更易于求解高维问题等的优点。径向基函数配点法的研究始于1990年[1],因为该方法的上述优点,日益引起诸多领域研究人员的关注。20世纪末至21世纪初该方法的理论基础初步建立[2,3,4,5,6],不过至那时以来相关的理论研究鲜有进展。与此同时,尝试将该方法应用于许多类型方程及许多工程领域问题的求解的报道越来越多[7,8,9,10].
类拉普拉斯方程是工程领域较为常见的一类偏微分方程,用径向基函数配点法按常规方法直接求解这类方程会因为方程本身的特征而失效。本文通过引入相容条件,建立了求解类拉普拉斯方程定解问题的径向基函数配点法,并用算例验证了该算法的有效性。
1 径向基函数配点法
径向基函数是指形如φ(‖x-ξ‖)这样的由一元函数与距离函数复合而成的函数,其中,ξ称为中心点。考虑如下微分方程定解问题:

其中,L为线性偏微分算子,f(x)、g(x)为已知函数。
布置中心点ξ={ξ1,…,ξN}和配点X={x1,…,xN}.将配点分成内点I(N0个点)和边界点B(N1个点)。用径向基函数构造如下形式的近似解函数,即
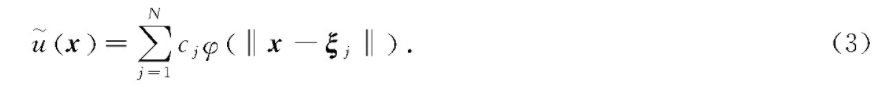
把近似解式(3)代入微分方程定解问题(1)、式(2)中,并使式(1)、式(2)分别在内点和边界点上成立,得到
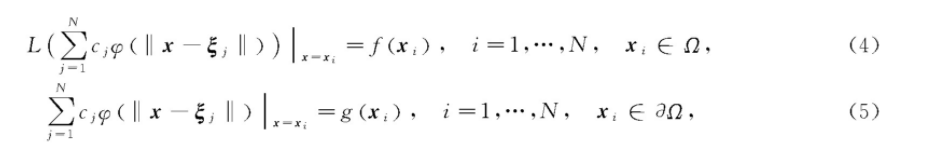
由此得到线性方程组

其中,
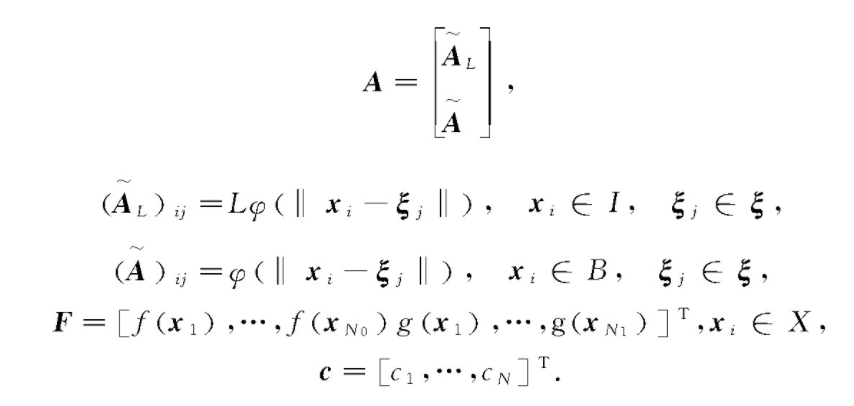
求解该方程组,由式(3)得到定解问题的近似解。
2 类拉普拉斯方程的径向基函数配点法
考虑如下形式的类拉普拉斯方程定解问题:
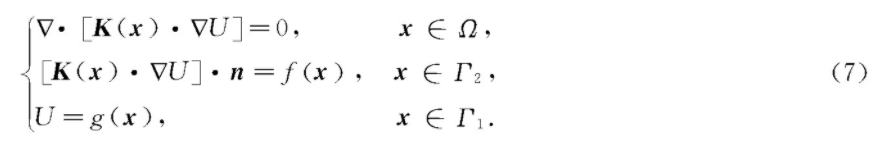
其中,U为待解函数,K为已知张量函数,n为外法线方向向量,f(x)和g(x)为已知函数,Γ1为第一类边界,Γ2为第二类边界。该方程常见于非均匀多孔介质中的单相稳态渗流问题,K是渗透率张量。如果U表示温度,K表示热传导系数,该方程就对应稳态热传导问题。
本文考虑K是分块常量的情形(这是数值计算时的典型情况)。依据K的分块特征将求解域划分为若干个子区域,使得K在每个子区域上为常量。以二维两个分区为例,如图1所示。
在不同子区域的分界线ΓD上满足相容条件,即
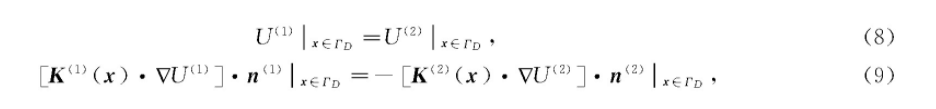
其中,U(i)为分界线上的i区待解函数,ni为i区的边界外法线方向,i=1,2.
如果取n=n(1),则n(2)=-n,式(9)变为
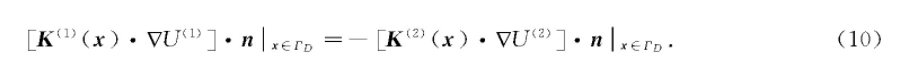
在此情况下,问题(7)可归结为如下的定解问题:
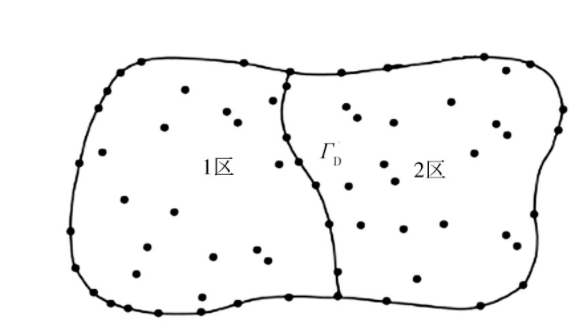
图1 分片常量区域图
Fig.1 Sharding constant region diagram
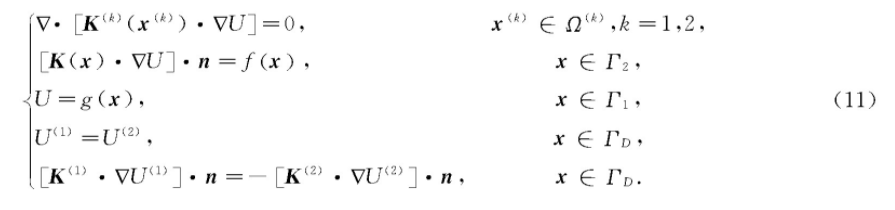
其中,Ω(k)为k区子域。
在1区、2区共布置N个中心点,并在1区、2区分别布置为k区内节点个数,N1(k)为k区一类边界节点个数,N2(k)为k区二类边界节点个数,M为两区分界线上节点个数。计算时,分界线上的节点既看作1区节点,也看作2区节点。
将近似解式(3)代入微分方程定解问题式(11)中,由式(4)、式(5)得到
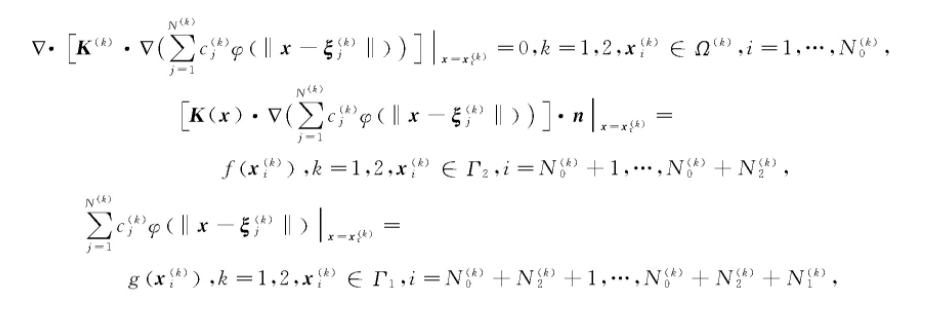
由式(6)得到近似解函数的待定系数在两个子区域满足的配点方程组(以下简称分区方程组):

其中,
将近似解式(3)代入相容条件式(8)、式(10)中,使代入后的相容条件式(8)、式(10)在分界线上的节点成立:
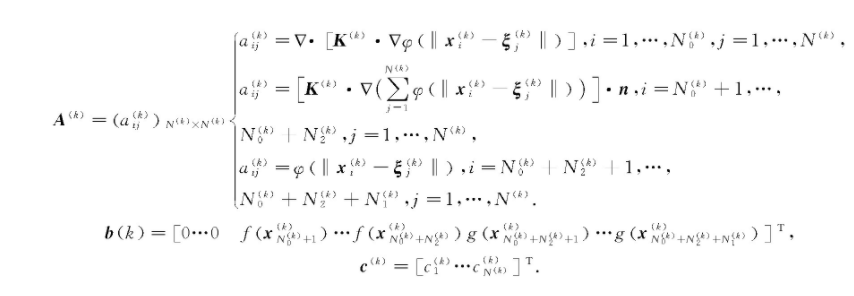
整理得到系数矩阵:
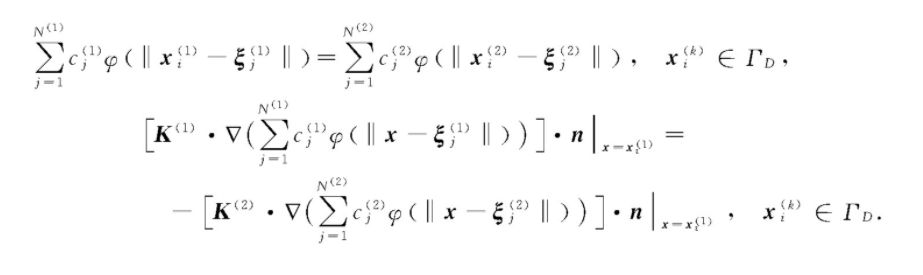
进而得到近似解函数的待定系数满足的配点方程组(以下简称相容条件方程组):

其中,A(k1)c(k)表示k区待解函数在分界线上节点的值,K(k)A(k2)c(k)表示分界线上k区外法线方向,
将分区方程组式(12)和相容条件方程组式(13)、式(14)联立得到定解问题式(11)的矩阵表达
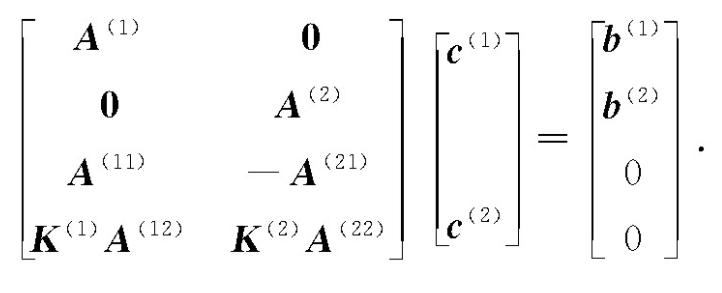
求解该方程组,就可以得到整个域上的近似解。
3 数值算例
假定区域Ω为矩形域0[,4]×0[,1],在矩形域Ω内满足
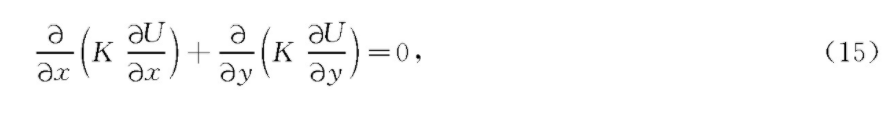
其中,
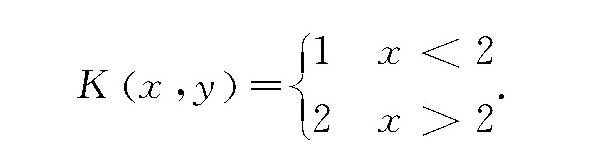
令式(15)的准确解是
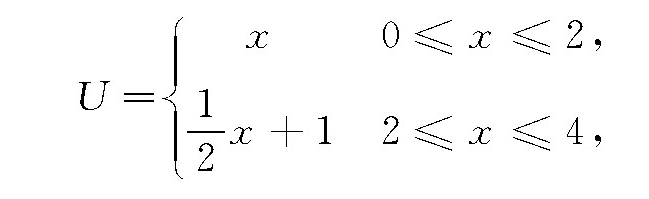
假定矩形域Ω的左右边界满足第一类边界条件,上下边界满足第二类边界条件,具体值由准确解确定。
求解该算例时,在Ω上均匀布置55个网格节点(xi,yi)作为中心点,分界线上的节点坐标分别为2(,0)2(,0.25)2(,0.5)2(,0.75)2(,1),中心点为节点坐标加MATLAB中的最小浮点数精度eps.取径向基函数选择为广义多二次函数:φr()=(1+(εr)2)52.取k区φr()中的ε为ε1=0.067,ε2=0.034,计算结果和准确解如图2,两者绝对误差如图3.
经检验,绝对误差为10-4数量级,算法具有较高的精度。
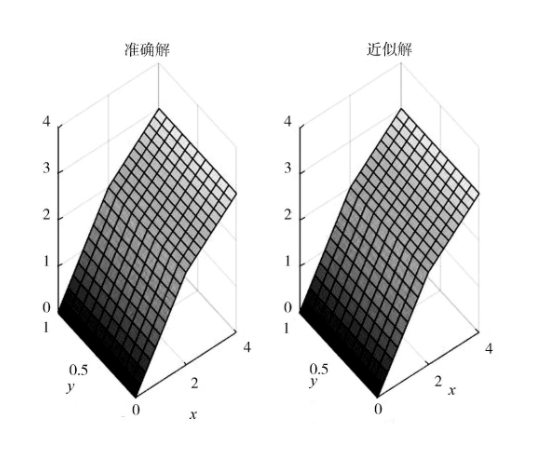
图2 准确解和近似解
Fig.2 Accurate and approximate solutions
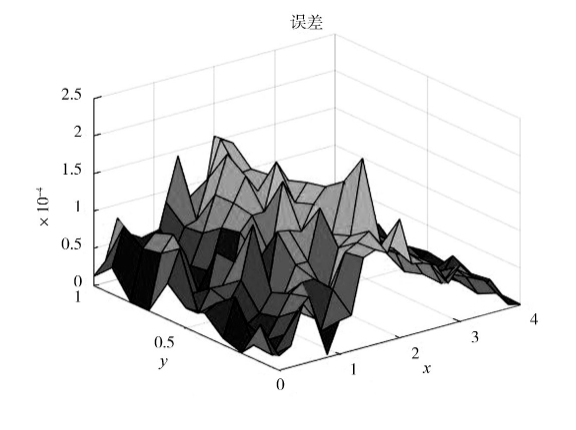
图3 准确解和近似解的绝对误
Fig.3 Absolute errors of the accurate and approximate solutions
4 结语
本文建立了径向基函数配点法求解类拉普拉斯方程问题的方法,算例计算表明该方法求解问题简捷有效,算法具有很高的精度。本文的方法具有节点布置灵活、完全不需要网格等优点,为类拉普拉斯方程问题的求解提供了一种新的途径。但在分区较多时,该方法就变得复杂了,失去其优越性。如何将该方法进行改进,使其易于求解较多分区的情况,将有待进一步研究。
参考文献
[1] KANSA E J.Multiquadrics-A scattered data approximation scheme with applications to computational fluid-dynamicsⅡ。Solutions to parabolic,hyperbolic and elliptic partial differential equations[J].Journal of Computational and Applied Mathematics,1990,19(8/9):147-161.
[2] KANSA E J,CARLSON R E.Improved accuracy of multiquadric interpolation using variable shape parameters[J].Journal of Computational and Applied Mathematics,1992,24(12):99-120.
[3] WU Z M,SCHABACK R.Local error estimates for radial basis function interpolation of scatered data[J].IMA Journal of Numerical Analysis,1993,13(1):13-27.
[4] WU Z M,HON Y C.Convergence error estimate in solving free boundary diffusion problem by radial basis functions method[J].Engineering Analysis with Boundary Elements,2003,27:73-79.
[5] FRANKE C,SCHABACK R.Solving partial differential equations by collocation using radial basis functions[J].Applied Mathematics and Computation,1998,93(1):73-82.
[6] CECILT,QIAN J L,OSHER S.Numerical methods for high dimensional Hamliton-Jacobi equations using radial basis functions[J].Journal of Computational Physics,2004,196:327-347.
[7] LORENTZ R A,NARCOWICH F J,WARD J D.Collocation discretizations of the transport equation with radial basis functions[J].Applied Mathematics and Computation,2003,145:97-116.
[8]SHIH Y T,TSAI K T,CHEN K T.Radial basis function collocation method for arotating Bose-Einstein condensation with vortex lattices[J].Interaction and Multiscale Mechanics,2012,5(2):131-144.
[9]ZHANG Y N,ZHANG H C,ZHANG X,et al.Block radial basis function collocation meshless method applied to steady and transient neutronics problem solutions in multi-material reactor cores[J].Progress in Nuclear Energy,2018,109:83-96.
[10]ZHENG H,ZHANG C,YANG Z.A local radial basis function collocation method for band structure computation of 3Dphononic crystals[J].Applied Mathematical Modelling,2020,77(Pt 2):1954-1964.





