摘要:本研究对象选择高机动型越野车,车架结构和车操控、安全、可靠、经济等性能息息相关。越野车行驶承受载荷也复杂,可导致车架扭转、弯曲以及变形等,刚度不足的区域可能出现裂纹。利用静态分析法,并使用惯性释放法,对于车架强度进行计算,将约束点反力应力以及变形问题产生的影响有效消除,保证该数据获取的精准性。
关键词:越野车; 车架; 有限元分析; 结构优化;
0 引言
我国的汽车技术资源相对匮乏,并且产业起步相对较晚,汽车生产之后,主要利用试验方式对于设计问题展开检验,不但耗时耗力,而且可靠性不高,存在较高风险。计算机技术的普及,有限元软件的应用,能够对于汽车、零件等展开分析,建立计算模型,通过模态分析掌握车架动态性能,进而对其结构加以优化。在振动理论不断发展过程中,越野车制造商高度关注动态仿真测试对于车身结构设计产生的影响。在越野车行驶过程,可受到动荷载,并且在时间不断推移之后,当外界的激励频率和某一零件或者整车的固有频率高度吻合,极易产生共振问题,致使车身材料出现疲劳失效这一问题。借助静力学以及动态特征展开仿真分析,结合分析结果,能够为越野车的结构优化以及整车性能的提升奠定良好基础。
1 有限元分析介绍
所谓有限元分析,主要是借助数学近似法,模拟几何图形以及荷载工况,并通过有限元单元对于真实系统展开分析,通过有限量探究未知量,甚至无限量。简单来讲,有限元分析的过程也是化繁为简的过程,使用大量简单函数替换复杂的函数模型。流程为先建模,之后将结构离散化,对单元以及整体展开分析。
2 越野车车架的有限元分析
2.1 模态分析
在高机动型越野车结构中,车架属于其承载系统,对于其展开模态分析,有助于研究人员了解车架振动特点,进而判断其是否和整车需求相符,避免出现设计、布局等缺陷,导致车身产生共振问题。对车架展开有限元分析,能够为其设计提供理论依据。按照模态分析这一理论,车架结构自振的频率和其结构阻尼矩阵以及外力等不相关,故此,分析越野车的车架模态时,无须将荷载问题考虑其中,将荷载以及约束条件去除[1]。
车架自由模态、约束模态二者之间存在高度相似性。分析其约束模态之时,需要将约束保留下来,但是在分析自由模态时,可使用其固有频率为频率分析标准。鉴于此,下文使用自由模态的方式进行分析。由于车架系统较为复杂,难以将其固有频率以及振型求出。结合模态分析理论,能够知晓车架结构动态特征,判断出其与地接振型存在关联。越野车的车身悬挂存在较大刚度,对于分析产生影响可忽略。在自由模态相关分析时,可提取车架当中6个振型,并对主振型展开描述:频率为28.7Hz时,为一阶扭转;频率为28.9Hz时,为一阶弯曲;频率为44.3Hz时,为面内一阶横摆;频率为52.1Hz时,为二阶扭转;频率为58.9Hz时,为二阶弯曲;频率为65.1Hz时,为二阶横摆。
2.2 分析结果
越野车行驶过程受到的外部激励主要有不平路面、发动机简谐等,因此,在展开车架的结构设计时,需要保证其固有频率和外界的激励频率之间相避开,以免车架结构产生共振的问题,进而防止车架的结构受到损坏。经过模态分析,按照结果能够精准识别出车架结构问题,并加以优化,将共振问题解决,保证车辆的行驶安全。
分析模态分析的结果,并将环境的激励频率考虑其中,结果如下:第一,路面条件通常能够决定路面激励。在高等公路以及高速公路路面,激励频率的变化范围在1~3Hz,因此,能够对于低频振动产生较大影响。下文研究的越野车车架产生的低阶频率高于路面存在的激励频率,因此,能够满足要求。第二,车架结构存在的固有模态,其频率不处于发动机的怠速运转产生的频率之内。结合公式F=n/60×M展开频率计算,公式当中M代表发动机缸数1/2,n代表发动机怠速实际转速。选取4缸发动机,怠速650r/min,经计算,频率结果等于21.6Hz,也就是怠速对于车架产生的激励频率是21.6Hz,对比于一阶扭转28.7Hz这一频率值,相对较低,因此,能够满足要求[2]。第三,车架的非簧载质量固有频率处于6~15Hz,由于本研究中确认第一阶扭转的频率值为28.7Hz,要远远高于车架固有频率,因此设计满足要求。第四,保证车架的振型保持光滑,以免产生突变。经过上述分析,能够确认,该车架的结构设计将外界激励频率区间有效避开,因此,动态性能良好。在车架模态分析过程,将静态分析的局限性有效克服,为整车舒适性以及平顺性等提供支持,并结合整车实际振动情况,完成车架优化及改进。
3 有限元分析下越野车车架结构优化
3.1 备胎支架方面
对于越野车的车架结构展开分析,选择其备胎支架当作研究对象,并完成拓扑结构的优化。汲取拓扑、结构等优化设计经验,以达到减重之效果。拓扑优化也可视为Opti Struct结构的优化,重点包括外形、尺寸、拓扑以及形状等内容。在拓扑优化的材料利用方面,可利用密度法,借助有限元模型,将各个空间单元视为设计变量,也称单元密度,此参数和结构材料相关,主要是从0~1之间选取连续的数值,经优化和求解以后,如果密度单元和1这个数值较为接近,或者等于1,则代表此单元位置材料十分重要,应该保留;如果单元密度数值和0接近,或者等于0,则代表此位置材料并不重要,能够去除,这样可保证该对于材料充分利用,完成轻量化设计[3]。
针对本文研究的越野车加的备胎支架展开拓扑优化,主要是在钣金件位置寻找最优的加强肋形状、位置等,在保持材料数量不改变的前提之下,将应力集中这一现象消除,与此同时,还能实现减重效果。选择质量35kg的备胎简化模型作为质量点,目的是将设计的空间体积保持在最低值[4]。选取空间单元作为设计变量,保持最大的应力约束达到235MPa,要求备胎支架产生的变形在5mm之内。在制动的工况之下,施加惯性荷载,X向为-1g,Z向为-1g;在转向工况之下,施加惯性荷载,Y向为1g,Z向为-1g;在垂直工况之下,施加惯性荷载,Z向为3.5g。设定参数之后,并利用密度法,以单元密度为设计变量,对于备胎支架结构加以优化,保持优化密度>0.5。图1为备胎支架拓扑优化结果图。
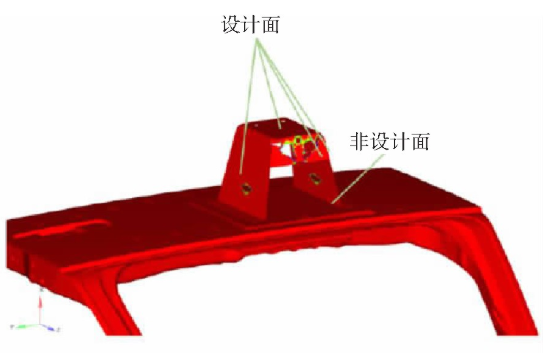
图1 备胎支架拓扑优化结果图
3.2 结构优化设计
按照拓扑的优化结果分析,背门固定面、备胎支架等所属非设计面,而备胎支架的侧面属于设计面。结合轻量化的设计,可使用两种优化方案,并且融合制动、转向、垂直冲击三种工况分别设计。
3.2.1 方案一
结合上文的分析结果,可使用增加减重区、减重孔等方式,实现车架的轻量化设计。优化方案如表1所示。
对拓扑结构进行优化之后,处理设计面,能够实现减重约43%。然而支架的最高应力和材料的屈服极限十分接近,特别是处于垂直工况时,支架承受的最高应力值高大235MPa,由此判断支架存在断裂的风险。因此,还需展开持续优化。
3.2.2 方案二
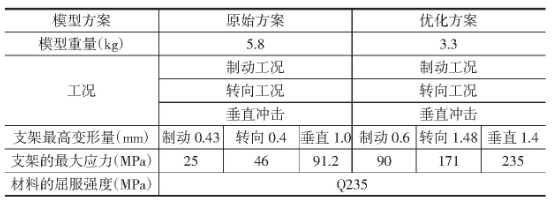
结合在方案一中的拓扑优化结果,在本优化方案当中,按照拓扑形貌、结构等优化设计经验,处于减重设计基础之上,可将减重孔面积增加,并且将冲压筋面增加,将支架实际受到的最大应力加以改善。使用上述设计之后,优化结果信息如表2所示。
表2 拓扑优化方案二结果表
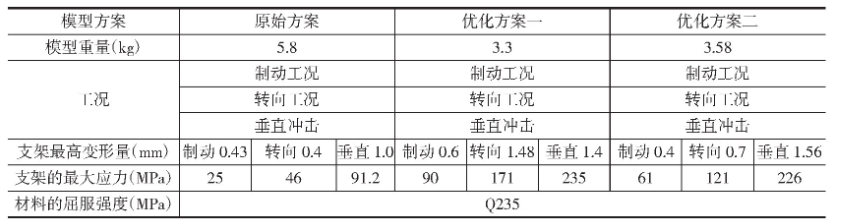
表1 拓扑优化方案一结果表
3.2.3 优化结果
结合上述优化设计结果,无论是使用方案一,还是使用方案二,都能和结构设计具体要求相符。但是,设计过程,还需将部件的局部安全系数这一因素考虑其中。对比而言,两种方案中,方案二更加精细化,成本相对较高,但是其应力结构的安全系数更高,因此,可选择方案二作为最终的优化结果,对比于最初的设计方案,可实现减重约38%。通过上述内容对于车架的备胎支架展开拓扑优化,经过两轮的试验分析,最终可达到设计要求,并实现轻量化的设计目的。
4 结束语
总之本研究对于某越野车的车结构设计展开分析,此车架的结构刚度、强度等良好,可满足空间的布置要求,整车越野性能优越。研究过程,针对车架结构建立有限元模型,并对于模型展开网格划分,保证有限元的计算精准。在分析车架刚度、强度等方面,借助惯性释放这一方法,选取车架6种典型的工况,并施加力矩,获得变形分布图,对于车架强度有效验证。并对于车架的模态展开分析,提取6个振型之下的模态结果,经过校核之后,对于车架动态特性展开验证,并为其舒适性的设计优化提供方向。在拓扑优化方面,选择备胎支架作为研究对象,结合有限元分析结果,完成优化设计,保证越野车车架的结构优化以及轻量化等前提之下,实现减重38%。
参考文献
[1] 程思远.基于有限元分析的汽车车架结构优化[J].汽车世界,2019(16):75-76.
[2]彭永子.汽车车架的有限元分析及优化设计研究[J].汽车实用技术,2018(22):49-51.
[3] 葛晗,陈鸿飞.多轴汽车车架结构强度有限元分析[J].百科论坛电子杂志,2018(09):270.
[4]刘巧珍,花豪.装载机前车架有限元分析与结构改进[J].建设机械技术与管理,2019(09):68-69.





